常见的数据分布(数据分布的类型)
本篇目录:
1、几种常见的数学分布2、常见分布有哪些?3、第三周:统计学之几种常见的数据分布4、数据分布的描述几种常见的数学分布
1、正态分布 若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。当μ = 0,σ = 1时的正态分布是标准正态分布。其中期望是u,方差是σ的平方。
2、均匀分布,期望是(a+b)/2,方差是(b-a)的平方/12。二项分布,期望是np,方差是npq。泊松分布,期望是p,方差是p。指数分布,期望是1/p,方差是1/(p的平方)。
3、八大常见分布的期望和方差如下:0-1分布:E(X)=p,D(X)=p(1-p)。二项分布B(n,p):P(X=k)=C(k\n)p^k·(1-p)^(n-k),E(X)=np,D(X)=np(1-p)。
4、六个常见分布的期望和方差:均匀分布,期望是(a+b)/2,方差是(b-a)的平方/12。二项分布,期望是np,方差是npq。泊松分布,期望是p,方差是p。指数分布,期望是1/p,方差是1/(p的平方)。
常见分布有哪些?
离散分布:伯努利分布(零一分布,两点分布),二项分布,几何分布,泊松分布(Poisson分布)。连续分布:指数分布,正态分布(高斯分布),均匀分布。抽样分布:卡方分布(X 2 分布),F分布,T分布。
六种常见分布的概率分布如下:离散型分布:0-1分布。只先进行一次事件试验,该事件发生的概率为p,不发生的概率为1-p 离散型分布:几何分布。在n次伯努利试验中,试验k次才得到第一次成功的概率。

六个常见分布的期望和方差:均匀分布,期望是(a+b)/2,方差是(b-a)的平方/12。二项分布,期望是np,方差是npq。泊松分布,期望是p,方差是p。指数分布,期望是1/p,方差是1/(p的平方)。
八大常见分布的期望和方差如下:0-1分布:E(X)=p,D(X)=p(1-p)。二项分布B(n,p):P(X=k)=C(k\n)p^k·(1-p)^(n-k),E(X)=np,D(X)=np(1-p)。
第三周:统计学之几种常见的数据分布
1、除正态分布之外,我们还经常会遇到其他一些比较常见的分布,如 t 检验对应的 t (T)分布, χ2 检验对应的 χ2 (X)分布、方差分析对应的 F (F)分布等。
2、正态分布(normal distribution)若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
3、三大分布是指来自正态总体三个常用分布,包括卡方分布、t分布和F分布。 数理统计 1-5章是公共部分,艺术和科学是科学,经济学和工程学都在学习。您是经济舱,而这个过程应该再学。其实,并不难学平稳随机过程,马尔可夫过程不是。
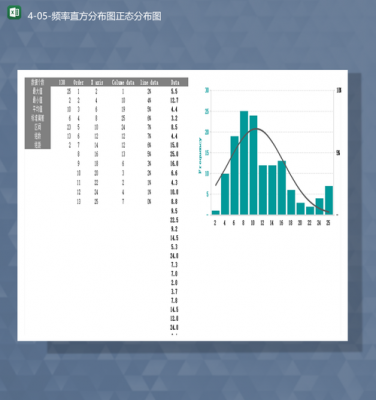
4、时间序列 其中条形图和饼图常用于描述分类型数据;直方图、茎叶图、时间序列图形常用于描述数值型数据 直方图,X轴表示数值的区间,Y轴表示该区间的数值个数。
5、详细解释:在统计学中,n数集也被广泛应用。例如,在描述数据分布时,可以使用n数集表示一组观测值的集合。通过对这些数据进行统计分析,可以得到关于数据的中心趋势、离散程度和分布形态等信息。
数据分布的描述
集中趋势的测度(众数、中位数、分位数、均值、几何平均数、切尾均值)。集中趋势又称“数据的中心位置”、“集中量数”等。它是一组数据的代表值。
数据分布的特征可以从三个方面进行测度和描述:一是:分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度。二是:分布的离散程度,反映各数据远离其中心值的趋势。三是:分布的形状,反映数据分布的偏态和峰态。
数据分布特征可以从集中趋势、离中趋势及分布形态三个方面进行描述。分布的集中趋势,反映各数据(众数、中位数、分位数、均值、几何平均数、切尾均值)向其中心值靠拢或聚集的程度。
描述一组数据的分布特征可以从数据分布集中趋势、数据分布离散程度、数据分布偏态与峰度的角度进行分析,平均指标是在反映总体的一般水平或分布的集中趋势的指标。集中趋势又称“数据的中心位置”、“集中量数”等。
到此,以上就是小编对于数据分布的类型的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。
-
无相关信息
- 1bat的大数据(BAT的大数据来源)
- 2三星s8屏幕上端2(三星s8屏幕上端2个按键)
- 3三星屏幕坏了如何导出(三星屏幕摔坏了如何导出数据么)
- 4红米3x怎么关闭自动更新(红米k40s怎么关闭自动更新)
- 5微信上防止app自动下载软件怎么办(微信上防止app自动下载软件怎么办啊)
- 6押镖多少钱(押镖一个月有多少储备金)
- 7瑞星个人防火墙胡功能(瑞星个人防火墙协议类型有哪些)
- 8cf现在等级是多少(cf等级2020最新)
- 9老滑头多少条鱼(钓鱼老滑头有什么用)
- 10WPS自动调整语法(wps如何修改语法)
- 11dell控制面板防火墙(dell的防火墙怎么关闭)
- 12丑女技能升多少(丑女技能需要满级吗)
- 13智能家居系统怎么样(智能家居系统好吗)
- 14戴尔屏幕(戴尔屏幕闪烁)
- 15y85屏幕信息(vivoy85息屏显示时间怎么设置)
- 16魅蓝note3屏幕出现方格(魅蓝note屏幕竖条纹)
- 17v8手指按屏幕(触屏手指)
- 18金为液晶广告机(液晶广告机lb420)
- 19三星显示器怎么校色(三星显示器 调色)
- 20hkc显示器dvi音频(hkc显示器有音响么)
- 21康佳液晶智能电视机(康佳液晶智能电视机怎么样)
- 22做液晶画板电脑(做液晶画板电脑怎么操作)
- 23液晶屏极化现象原理(液晶屏极化现象原理是什么)
- 24企业网络安全防火墙(企业网络防护)
- 256splus黑屏屏幕不亮(苹果6s plus屏幕突然黑屏)
- 26充电导致屏幕失灵(充电导致屏幕失灵怎么办)
- 27超极本屏幕旋转(笔记本电脑屏幕旋转,怎么转过来?)
- 28igmp防火墙(防火墙配置ipv6)
- 29荣耀王者多少经验(王者荣耀经验多少一级)
- 30lol老将还剩多少(qg老将)