正态分布数据(正态分布数据如何描述)
本篇目录:
1、检验数据是否为正态分布2、正态分布的3个数值3、什么是正态分布4、如何用中值估计正态分布数据的标准差?5、正态分布中的数据有什么特点?6、正态分布的数据怎么看?检验数据是否为正态分布
1、正态性检验:偏度和峰度。偏度(Skewness):描述数据分布不对称的方向及其程度。
2、正态概率图(PP图):通过将样本值按从小到大排序,并将其对应的分位数与正态分布的分位数进行比较,来判断样本的分布是否近似于正态分布。如果点符合一条直线,则说明该数据集呈现正态分布。
3、样本是不是正态分布的检验方法:偏度和峰度,图示法,非参数检验。偏度和峰度 偏度:描述数据分布不对称的方向及其程度。
正态分布的3个数值
正负3个标准差,即(μ-3σ,μ+3σ)区间内,面积为974%.这是由正态分布的性质所决定的。
正态分布是具有两个参数μ和σ^2的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ^2 )。
正态分布有两个参数,即均数μ和标准差σ,可记作N(μ,σ)。若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。

什么是正态分布
正态分布具有两个参数μ和σ^2的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ2)。
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。
正态分布(也称为高斯分布)的概率密度函数(Probability Density Function,简称 PDF)是一个常见的统计分布函数,通常用来描述连续型随机变量的分布情况。
正态分布(Normal distribution)是一种概率分布。

正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
正态分布就是大部分属于中间值,只有一小部分属于过大和过小的值,它们分布在范围的两端。
如何用中值估计正态分布数据的标准差?
1、对正态分布密度函数下进行积分就行了,对整个实数域积分的结果肯定等于1,而对任意有界区域积分的结果一般情况下只能进行近似的数值计算,而不能给出解析表达式。
2、在正态分布中σ代表标准差,μ代表均值。x=μ即为图像的对称轴。
3、所有数减去其平均值的平方和,所得结果除以该组数之个数(或个数减一,即变异数),再把所得值开根号,所得之数就是这组数据的标准差。
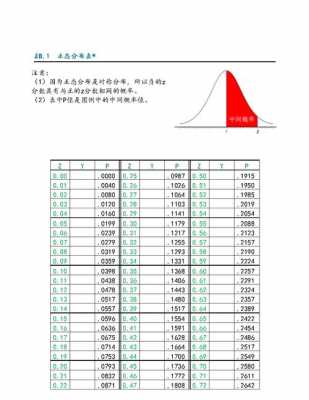
4、第一步、首先要了解标准正态分布的公式,如下图所示。第二步、假设X=15,首先在左边一列找到1(如图);第三步、在上面一行找到0.05,如下图所示。
5、正态分布的标准差正态分布N~(μ,duδ^2),方差D(x)=δ^2,E(x)=μ。服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值。
6、正态分布标准差的概率意义:我们可以从上一步图中看出,观察值x落在[μ-σ,μ+σ],[μ-2σ,μ+2σ],[μ-3σ,μ+3σ]区间的概率,即P(μ-k·σ≤x≤μ+k·σ)分别是0.68269,0.9545,0.9973。
正态分布中的数据有什么特点?
1、正态分布具有两个参数μ和σ^2的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ2)。
2、正态分布(也称为高斯分布或钟形曲线)是统计学中最重要的分布之一,具有以下特征:对称性、单峰性、定义明确的均值和标准差、所有正态分布的两个特殊参数、中心极限定理、知名特性。
3、它具有以下特点:对称、单峰、平均值等于中位数等。正态分布是具有两个参数μ和σ2的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差,所以正态分布记作N(μ,σ2)。
4、正态分布的特点:正态分布满足以下特点:- 对称性:正态分布的曲线在均值处对称,左右两侧的概率相等。- 峰度(Kurtosis):正态分布的峰度较高,曲线在均值附近较为陡峭。
正态分布的数据怎么看?
1、所谓的正态分布表都是标准正态分布表(n(0,1),通过查找实数x的位置,从而得到p(z=x)。表的纵向代表x的整数部分和小数点后第一位,横向代表x的小数点后第二位,然后就找到了x的位置。
2、偏度(Skewness):描述数据分布不对称的方向及其程度。
3、标准正态分布表中的数值代表该数值以下(或以上)的概率。例如在表中查得0.5,表示在标准正态分布中,取值小于0或大于0.5的概率是0.5。也就是说,如果你随机抽取一个数,这个数小于0或大于0.5的概率是0.5。
到此,以上就是小编对于正态分布数据如何描述的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。
-
无相关信息
- 1bat的大数据(BAT的大数据来源)
- 2三星s8屏幕上端2(三星s8屏幕上端2个按键)
- 3三星屏幕坏了如何导出(三星屏幕摔坏了如何导出数据么)
- 4红米3x怎么关闭自动更新(红米k40s怎么关闭自动更新)
- 5微信上防止app自动下载软件怎么办(微信上防止app自动下载软件怎么办啊)
- 6押镖多少钱(押镖一个月有多少储备金)
- 7瑞星个人防火墙胡功能(瑞星个人防火墙协议类型有哪些)
- 8cf现在等级是多少(cf等级2020最新)
- 9老滑头多少条鱼(钓鱼老滑头有什么用)
- 10WPS自动调整语法(wps如何修改语法)
- 11dell控制面板防火墙(dell的防火墙怎么关闭)
- 12丑女技能升多少(丑女技能需要满级吗)
- 13智能家居系统怎么样(智能家居系统好吗)
- 14戴尔屏幕(戴尔屏幕闪烁)
- 15y85屏幕信息(vivoy85息屏显示时间怎么设置)
- 16魅蓝note3屏幕出现方格(魅蓝note屏幕竖条纹)
- 17v8手指按屏幕(触屏手指)
- 18金为液晶广告机(液晶广告机lb420)
- 19三星显示器怎么校色(三星显示器 调色)
- 20hkc显示器dvi音频(hkc显示器有音响么)
- 21康佳液晶智能电视机(康佳液晶智能电视机怎么样)
- 22做液晶画板电脑(做液晶画板电脑怎么操作)
- 23液晶屏极化现象原理(液晶屏极化现象原理是什么)
- 24企业网络安全防火墙(企业网络防护)
- 256splus黑屏屏幕不亮(苹果6s plus屏幕突然黑屏)
- 26充电导致屏幕失灵(充电导致屏幕失灵怎么办)
- 27超极本屏幕旋转(笔记本电脑屏幕旋转,怎么转过来?)
- 28igmp防火墙(防火墙配置ipv6)
- 29荣耀王者多少经验(王者荣耀经验多少一级)
- 30lol老将还剩多少(qg老将)