判别分析数据（判别分析数据案例）

本篇目录：

1、判别分析的基本思想2、如何使用SPSS进行一般判别分析3、判别分析(Fisher判别方法)4、什么是判别分析?如何应用?5、常用的主流数据统计分析方法:2.判别分析6、20数据判别分析

判别分析的基本思想

1、Fisher判别分析的基本思想 ：选取适当的投影方向，将样本数据进行投影，使得投影后各样本点尽可能分离开来，即：使得投影后各样本 类内 离差平方和尽可能小，而使各样本 类间 的离差平方和尽可能大。

2、）距离判别：其基本思想是有训练样品得出每个分类的重心坐标，然后对新样品求出它们离各个类别重心的距离远近，从而归入离得最近的类。也就是根据个案离母体远近进行判别。最常用的距离是马氏距离，偶尔也采用欧式距离。

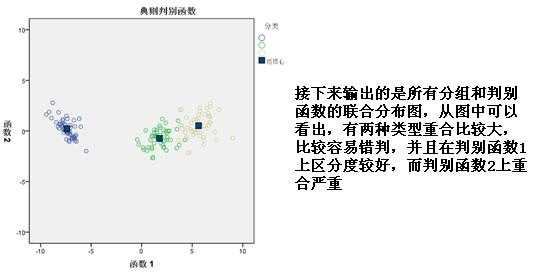
3、Fisher线性判别分析的基本思想：选择一个投影方向（线性变换，线性组合），将高维问题降低到一维问题来解决，同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起，不同类的样本相隔尽可能地远。

如何使用SPSS进行一般判别分析

1、在这种一部分数据缺失的情况下，我们就可以利用SPSS的判别分析来对缺失数据进行分析补充，也就是这里提到的一般判别分析。

2、通过快捷方式，打开SPSS分析工具，默认显示在数据编辑器。点击变量视图，添加两个变量分类（字符串类型）和数量（数值类型）。切换到数据视图，在分类和数量两列添加数据。点击工具栏中的数据，然后选择拆分文件。

3、的线性判别式函数系数为贝叶斯的线性判别函数系数(可见课本第五版课本P123)，这是用贝叶斯判别分析法产生的分类函数系数，可见课本第五版课本P121的17式，可以计算出每个观测在各组的分类函数值，然后将观测分类到较大的分类函数值中。

4、步骤如下：我们在打开SPSS软件后会出现两个界面，如下图；图1：是数据处理分析区，包括数据视图（数据处理区）和变量视图（数据包含各字段编辑区）。图2：是分析结果区，分析的各类结果都会在此显示。

5、线性模型；点击分析，一般线性模型，单变量，设置因变量和固定因子，点击确定即可。图表分析。回归分析，点击分析，打开回归，设置自变量和因变量数据，点击确定即可。直方图分析。统计分析。

6、通过analyze下面的regression来完成。即把农民收入选进因变量，其他（除年份和总计）作为自变量分析。当然里面还有像statistics等这些功能项，你作为默认就行了。第三步：解释模型。

判别分析(Fisher判别方法)

1、Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值w0， 即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。Fisher判别分析是要实现有最大的类间距离，以及最小的类内距离。

2、fisher判别方法的主要特点是先对数据进行投影然后再利用距离进行判别。

3、建立模型的方式不同。Fisher判别分析是一种基于统计学原理的线性分类方法，通过寻找最佳投影方向，将原始特征空间映射到一个新的低维度特征空间中，并在新的特征空间中寻找一个最优决策面来进行分类。

4、怎么做fisher判别分析？卡方检验研究数据的独立性，在分析样本量较少（比如小于40），也或者期望频数出现小于5时，此时使用fisher卡方检验较为适合。

5、已知有A类和B类两类观察对象，A类有a例，B类有b例，分别记录了X1，X2，……Xm个观察指标，我们称这m个观察指标为判别指标或变量。

6、Fisher判别分析的基本思想 ：选取适当的投影方向，将样本数据进行投影，使得投影后各样本点尽可能分离开来，即：使得投影后各样本 类内 离差平方和尽可能小，而使各样本 类间 的离差平方和尽可能大。

什么是判别分析?如何应用?

判别分析最初应用于考古学， 例如要根据挖掘出来的人头盖骨的各种指标来判别其性别年龄等.。慢慢的成为一种常用的分类分析方法，其通过已知的分类情况，根据数据的特征对其他研究对象进行预测归类。

判别分析是在分组已知的情况下，根据已经确定分类的对象的某些观测指标和所属类别来判断未知对象所属类别的一种统计学方法。

所谓回归分析，是指一种表述自变量对因变量影响的公式技术。如果在回归分析中，统计方程式只涉及一个自变量，我们称该方程式为简单回归；如果涉及两个或两个以上自变量，我们称该统计方程式为多元回归。（2）判别分析。

a. 目的 ：识别一个个体所属类别 b. 适用 ：被解释对象是非度量变量（nonmetric），解释变量是度量变量；分组类型2组以上，每组样品1。

判别分析，是一种统计判别和分组技术，就一定数量样本的一个分组变量和相应的其他多元变量的已知信息，确定分组与其他多元变量信息所属的样本进行判别分组。

问题一：判别分析的应用 在气候分类、农业区划、土地类型划分中有着广泛的应用。在市场调研中，一般根据事先确定的因变量(例如产品的主要用户、普通用户和非用户、自有房屋或租赁、电视观众和非电视观众)找出相应处理的区别特性。

常用的主流数据统计分析方法:2.判别分析

1、聚类分析：聚类分析以多个研究标题作为基准，对样本对象进行分类。如果是按样本聚类，则使用SPSSAU的进阶方法模块中的“聚类”功能，系统会自动识别出应该使用K-means聚类算法还是K-prototype聚类算法。

2、对比分析法 对比分析法，是将两个或两个以上的数据进行对比，分析差异进而揭示这些数据所代表的规律。对比分析法包括横向比较及纵向比较。

3、对比分析 对比法就是用两组或两组以上的数据进行比较，是最通用的方法。 我们知道孤立的数据没有意义，有对比才有差异。比如在时间维度上的同比和环比、增长率、定基比，与竞争对手的对比、类别之间的对比、特征和属性对比等。

4、对比分析法：常用于对纵向的、横向的、最为突出的、计划与实际的等各种相关数据的。例如：今年与去年同期工资收入的增长情况、3月CPI环比增长情况等。

20数据判别分析

1、、在正态等协差阵的条件下，Bayes 判别法（不考虑先验概率的影响）等价于距离判别准则和 Fisher 线性判别法。 3 、当 K 个总体的均值向量共线性较高时，Fisher 判别法可用较少的判别函数进行判别。

2、（1）医学诊断：通过对疾病相关因素的分析和判别，确定患者的病情和治疗方案。（2）金融风险评估：通过对客户信用记录、财务状况等因素的分析和判别，确定客户的信用等级和贷款风险。

3、此数据是判别分析中经典的案例数据。该数据是利用花萼长、花萼宽、花瓣长、花瓣宽共4个特征，来预测花的种类（共3类：分别是刚毛鸢尾花、变色鸢尾花和佛吉尼亚鸢尾花；下面全部是类别1，类别2和类别3表示）。

4、iii. 判别准则： i. 个体归属某类的概率（后验概率）最大 ii. 错判总平均损失最小为标准。 vi. 贝叶斯判别的后验概率最大 i. 贝叶斯（Bayes）判别要变量服从 正态分布 类型。

5、数据输入 [if ！vml] [endif] 操作步骤 进入SPSS，打开相关数据文件，选择“分析”|“分类 ”|“判别式”命令选择进行判别分析的变量。在“判别分析”对话框的左侧列表框中，选择“类型”进入“分组变量”列表框。

6、高级的分析方法 有：相关分析法、回归分析法、聚类分析法、判别分析法、主成分分析法、因子分析法、对应分析法、时间序列等。 懂工具。指掌握数据分析相关的常用工具。

到此，以上就是小编对于判别分析数据案例的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。

数据